Introduction

Forward propagation is a pivotal aspect of AI, encompassing the process through which data traverses various layers to produce an output. Despite its apparent simplicity, this is a fundamentally intricate procedure. At its core, forward propagation is a mathematical model comprising input layers, hidden layers, and an output layer. Within each layer, neurons are interconnected with the preceding and succeeding layers, establishing a complex network. Furthermore, each neuron is characterized by connections to previous layer neurons and an activation link to the subsequent layer.

Let's start from math

Each neuron comprises a bias, input data, weight, and output data. The image below illustrates its components.

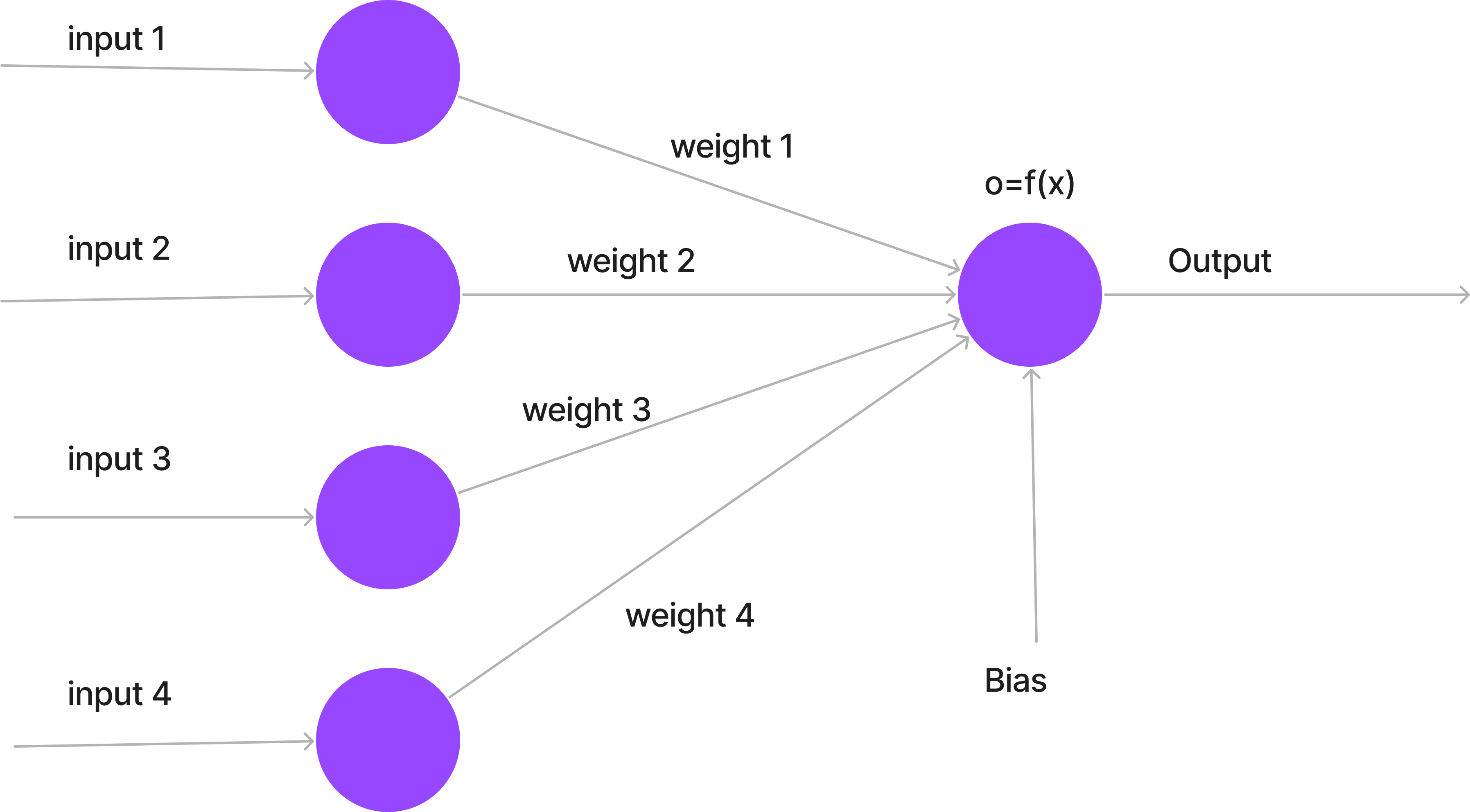
The formula governing the neuron's behavior is straightforward:

x = input1 * weight1 + input2 * weight2 + input3 * weight3 + input4 * weight4 + bias

Here, x represents the weighted sum of inputs, and the activation function f(x) produces the output.

So, what is an activation function? Essentially, it is a function that normalizes the output for the next neuron. The activation function plays a crucial role in the neuron model as it determines whether the next neuron will receive an inactive value (0) or an active value different from zero.

Various functions can be employed as activation functions, including ReLU, Binary Step, Sigmoid, TanH, and others. Detailed information about these functions can be found here.

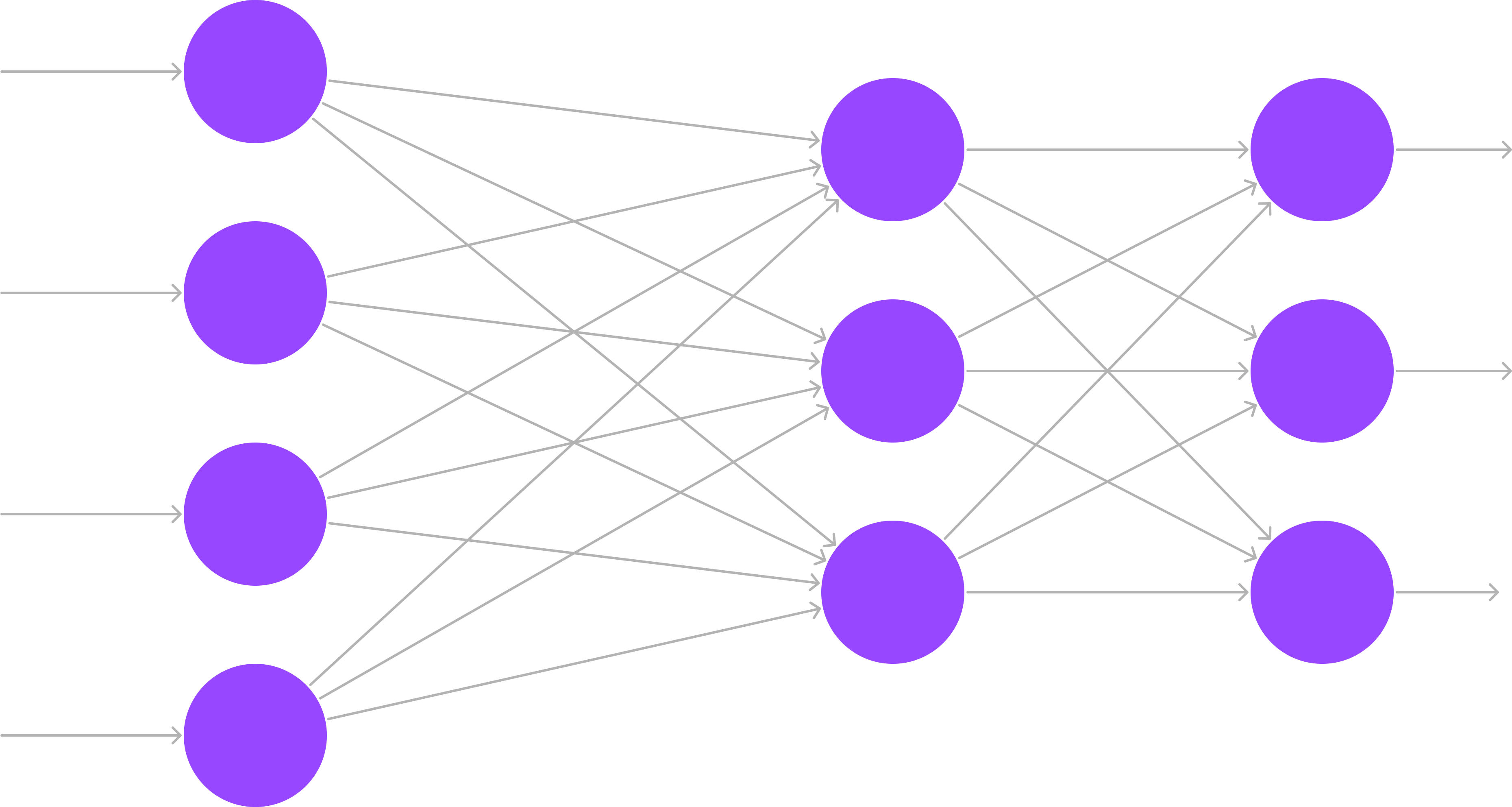
All together neural network looks like this

Let's try to do some coding and start from neuron using C#

public class Neuron
{
    private double _bias = 0.05;

    private readonly IEnumerable<double> weights;

    public Neuron(IEnumerable<double> weights) => this.weights = weights;

    public double Forward(double[] input)
    {
        var x = weights.Select((e, i) => e * input[i]).Sum() + _bias ;
        return HyperbolicTangent(x);
    }

    private double HyperbolicTangent(double x)
    {
        return x < -45.0 ? -1.0 : x > 45.0 ? 1.0 : Math.Tanh(x);
    }
}

These adjustments aim to improve the clarity of your code. Feel free to make further modifications according to your preferences and specific requirements. Now that we have implemented the neuron, we can proceed to add our layer.

Next step is to make Layer from collection of neurons, apart from that I'm planning to initialize each weight by basic value using InitializeWeights(int) method.

public class Layer
{
    private static readonly Random _random = new();

    private readonly Neuron[] _neurons;

    public Layer(int inputSize, int neuronSize)
    {
        _neurons = Enumerable.Range(0, neuronSize)
        .Select(_ => new Neuron(InitializeWeights(inputSize))).ToArray();
    }

    public double[] Forward(double[] input) 
        => _neurons.Select(e => e.Forward(input))
          .ToArray();

    private static double[] InitializeWeights(int length) 
        => Enumerable.Range(0, length).Select(_ => _random.NextDouble())
           .ToArray();
}

In our current implementation, we have a neural network with only one layer. However, neural networks are mathematical models designed with multiple layers, each connected to the next. Let's take a step towards a more complex network by implementing a simple class that follows this layered approach.

public class NeuronNetwork
{
    private readonly Layer[] _layers;
    public NeuronNetwork(int layers, int inputs, int outputs)
    {
        _layers = new Layer[layers];
        Init(inputs, outputs);
    }

    private void Init(int inputs, int outputs)
    {
        _layers[0] = new Layer(inputs, 16);
        _layers[1] = new Layer(16, 16);
        for(int i = 2; i < _layers.Length - 1; ++i)
        {
            _layers[i] = new Layer(16, 16);            
        }
        _layers[_layers.Length - 1] = new Layer(16, 10);   
    }

    public double[] Forward(double[] inputs)
    {
        double[] result = inputs;
        for(var i = 0; i < _layers.Length; ++i)
        {
            result = _layers[i].Forward(result);
        }
        return result;
    }
}

The NeuronNetwork class is straightforward to explain. It consists of two essential methods. The first, Forward, iterates through each layer, passing and refining the input. The second method, InitializeLayers, is not strictly necessary, serving only for the initialization of all layers. Despite its simplicity, the Forward method is crucial as it represents the decision-making process within the neural network.

And the final usage might look like below code

double[] neuronInput = new double[] 
{
    1, 0, 0, 0, 1, 2, 3, 4, 5, 6, 12, 
    3, 4, 5, 6, 7, 8, 3, 4, 5, 3, 4, 5, 6, 4, 6
};

var neuronNetwork = new NeuronNetwork(5, neuronInput.Length, 11);
var result = neuronNetwork.Forward(neuronInput);

The result will be similar to be below output

0.9999996050443055
0.9999987630645377
0.9999999832777687
0.9999999781899126
0.9999995935155542
0.9999996536802952
0.999999963953007
0.999998616978532
0.9999865241811555
0.9999996568361271

While the output may not necessarily align with the expected result, it's important to note that we have only implemented forward propagation. To further enhance the performance of our model, we need to introduce a new chapter: Backward Propagation. This technique enables the model to refine its internal values for biases and weights. Consequently, after each iteration, adjustments are made based on our expectations or, simply put, during the training process.

Conclusion

In embarking on a simple implementation of a neural network, it becomes essential to comprehend the workings of the Input Layer, Hidden Layer, Output Layer, Weights, and Biases. Understanding the necessity and role of Activation Functions further contributes to this foundational knowledge. The next steps involve delving into the realms of learning and optimization, which we'll explore in the upcoming chapter.